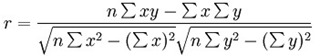1、协方差矩阵
- 协方差是衡量两个随机变量(同一样本,不同分量)的相关程度。(方差描述的是一维变量)
- 随机变量 之间的协方差可以表示为
- 根据已知的样本值可以得到协方差的估计值如下(列向量相关):
- 可以进一步地简化为:
- 协方差矩阵:
- 说明:
(1)协方差矩阵中的每一个元素是表示的随机向量X的不同分量之间的协方差(不同维数的相关性,即列向量的相关性),是个对称矩阵,而不是不同样本之间的协方差,如元素Cij就是反映的随机变量Xi, Xj的协方差。
(2)协方差是反映的变量之间的二阶统计特性,如果随机向量的不同分量之间的相关性很小,则所得的协方差矩阵几乎是一个对角矩阵。对于一些特殊的应用场合,为了使随机向量的长度较小,可以采用主成分分析的方法,使变换之后的变量的协方差矩阵完全是一个对角矩阵,之后就可以舍弃一些能量较小的分量了(对角线上的元素反映的是方差,也就是交流能量)。特别是在模式识别领域,当模式向量的维数过高时会影响识别系统的泛化性能,经常需要做这样的处理。
(3)求协方差矩阵的matlab函数:cov
2、相关矩阵
- 相关系数:
著名统计学家卡尔·皮尔逊设计了统计指标——相关系数。相关系数是用以反映变量之间相关关系密切程度的统计指标。相关系数是按积差方法计算,同样以两变量与各自平均值的离差为基础,通过两个离差相乘来反映两变量之间相关程度;着重研究线性的单相关系数。
依据相关现象之间的不同特征,其统计指标的名称有所不同。如将反映两变量间线性相关关系的统计指标称为相关系数(相关系数的平方称为判定系数);将反映两变量间曲线相关关系的统计指标称为非线性相关系数、非线性判定系数;将反映多元线性相关关系的统计指标称为复相关系数、复判定系数等。
相关系数用r表示,它的基本公式(formula)为:
- 相关系数的值介于–1与+1之间,即–1≤r≤+1。其性质如下:
当r>0时,表示两变量正相关,r<0时,两变量为负相关。
当|r|=1时,表示两变量为完全线性相关,即为函数关系。
当r=0时,表示两变量间无线性相关关系。
当0<|r|<1时,表示两变量存在一定程度的线性相关。且|r|越接近1,两变量间线性关系越密切;|r|越接近于0,表示两变量的线性相关越弱。
一般可按三级划分:|r|<0.4为低度线性相关;0.4≤|r|<0.7为显著性相关;0.7≤|r|<1为高度线性相关。
- 相关矩阵也叫相关系数矩阵,是由矩阵各列间的相关系数构成的
- 也就是说,相关矩阵第i行第j列的元素是原矩阵第i列和第j列的相关系数
- 求取相关矩阵的matlab函数为:correoff
3、协方差矩阵和相关矩阵的关系
由二者的定义公式可知,经标准化的样本数据的协方差矩阵就是原始样本数据的相关矩阵。这里所说的标准化指正态化,即将原始数据处理成均值为0,方差为1的标准数据。
即:
X'=(X-EX)/DX
用matlab函数表达为:
X'=zscore(X)
则协方差矩阵和相关矩阵的关系可表达为:
correoff(X)=cov(zscore(X))