當前位置：首頁 > news >簡體>「動態規劃::狀壓DP」網格圖遞推 / AcWing 292|327（C++）

「動態規劃::狀壓DP」網格圖遞推 / AcWing 292|327（C++）

news 來源：原創 2025/6/23 5:17:46

概述

相鄰行遞推

思路

算法過程

優化方案

空間優化

返回值優化

Code

復雜度

相鄰兩行遞推

思路

算法過程

Code

復雜度

特殊優化：編譯期計算

總結

概述

如果我們有一張地圖，要求是在符合某類條件的前提在地圖上放置最優解，該怎么計算？

這也屬于狀壓dp的應用之一。

相鄰行遞推

AcWing 237：

農夫約翰的土地由?M×N 個小方格組成，現在他要在土地里種植玉米。

非常遺憾，部分土地是不育的，無法種植。

而且，相鄰的土地不能同時種植玉米，也就是說種植玉米的所有方格之間都不會有公共邊緣。

現在給定土地的大小，請你求出共有多少種種植方法。

土地上什么都不種也算一種方法。

輸入格式

第?1?行包含兩個整數?M?和?N。

第?2..M+1 行：每行包含?N?個整數?0?或?1，用來描述整個土地的狀況，1?表示該塊土地肥沃，0?表示該塊土地不育。

輸出格式

輸出總種植方 1e8 取模后的值。

數據范圍

1≤M,N≤12

輸入樣例：
2 3
1 1 1
0 1 0
輸出樣例：
9

思路

之所以可以進行狀壓dp是因為列的數量較小，我們可以把一行壓縮成一個整數。

也就是說我們有地圖狀態 g[i] = (10011) $^{_{2}}$ ，?意味著第 i 行的第0、1、4列可以種植。

我們發現需要兩個狀態：當前行序號和當前行內種植的情況。

定義 dp[i][k]，表示[0,?i] 行內且第 i 行狀態為 k 的種植方案數，例如：

若 k =?(10001) $^{_{2}}$ ，意味著第 i 行的種植了第0、4列。

那么dp[i][k]可以從什么轉移來呢？我們發現有以下約束：

k 要服從地圖的約束，也就是第 i 行的合法 k 僅能是 g[i] 的子集。
k 內不含有相鄰1，也就是行內需要合法。
第 i 行 k 也不能與 i - 1 行 k 不含有相鄰1，也就是行間需要合法。

基于此，我們可以得知轉移方程： dp[i][k] =? $\sum$ dp[i - 1][t]。

其中，k、t 都行內合法且符合地圖約束，且 k 與 t 行間兼容。?

初始條件下，dp[0][服從地圖0行的k] = 1。

算法過程

可以預處理出合法的 k。

行內合法的條件是：?(k & (k >> 1) == 0。什么意思呢？k 的二進制位右移1位，與原來的 k 作與運算，就是試圖讓相鄰的1重疊在一起，若真的有相鄰的1，那么與運算結果必不為0。

為什么不用考慮左移呢？因為對于相鄰的11，右1左移和左1右移是一樣的。

如果你糾結于右移的溢出位的話，可以將二進制串前后補上無限長的0，再感受一下。

符合地圖約束的k的條件：(k | g[i]) == g[i]。意味著k是g[i]的子集。
行間合法的條件是：(k1 & k2) == 0。意味著二者無重合的1，作為上下行時，就沒有相鄰的1。

那代碼大概是這樣的：?

int solve(){for (int k = 0; k <= mx; k++)if (!(k & (k >> 1)))st.push_back(k);for (int k : st)if ((k | g[0]) == g[0])dp[0][k] = 1;for (int i = 1; i < m; i++)for (int k : st) if((k | g[i]) == g[i])for (int pre_k : st) if (!(k & pre_k) && (pre_k | g[i - 1]) == g[i - 1])dp[i][k] = (dp[i][k] + dp[i - 1][pre_k]) % MOD;int ans = 0;for (int k : st)ans = (ans + dp[m - 1][k]) % MOD;return ans;
}

優化方案

空間優化

注意到dp[i]總是來自上一行dp[i - 1]，所以可以做一層空間優化。

僅使用兩行儲存dp，怎么區分哪行是上一行，哪行是這一行呢？

注意到枚舉 i 時， i 的奇偶性持續發生變化，我們用 i & 1 作索引，dp[i & 1]儲存第 i 行，dp[(i - 1) & 1] 就是上一行，當開始計算dp[i & 1][k]時，要先置 0 ，清除上上行的狀態。

返回值優化

在最后，我們選擇 i 多枚舉1行，即計算到 i == m，此時答案就儲存在?dp[m & 1][0]中，即 m 行，那個不存在的行，放置情況是0時即全空，這時的總狀態。

Code

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 13, MOD = 1e8;
int m, n, mx;
int g[N], dp[2][1 << N];
vector<int> st;
int solve(){for (int k = 0; k <= mx; k++)if (!(k & (k >> 1)))st.push_back(k);for (int k : st)if ((k | g[0]) == g[0])dp[0][k] = 1;for (int i = 1; i <= m; i++)for (int k : st) if((k | g[i]) == g[i]) {dp[i & 1][k] = 0;for (int pre_k : st) if (!(k & pre_k) && (pre_k | g[i - 1]) == g[i - 1])dp[i & 1][k] = (dp[i & 1][k] + dp[(i - 1) & 1][pre_k]) % MOD;}return dp[m & 1][0];
}
int main(){cin >> m >> n;  mx = (1 << n) - 1;for (int i = 0; i < m; i++)for (int j = 0; j < n; j++) {int x; cin >> x;g[i] |= x << j;}cout << solve();return 0;
}

復雜度

時間復雜度:?O(?+? $m(\frac{1 + \sqrt{5}}{2}) ^{n}$ )

空間復雜度:?O( $2^{n}$ )?

n：列數

m：行數

復雜度分析：

時間分析：{

枚舉合法 k ，O()。

求合法 k 的數目：n 位不含有連續1的二進制數，設為 cnt(n)。

設 a[n] 表示 n 位不含有連續1且末位為1的二進制數數目，b[n] 表示 n 位不含有連續1且末位為0的二進制數數目。

則 cnt(n) = a[n]?+ b[n]。

其中 a[n] =?b[n - 1]，b[n] = a[n - 1] + b[n - 1] = cnt(n - 1)。（前位為1則末位為0，前位為0則末尾任意）

則 cnt(n) = a[n]?+ b[n] = b[n - 1]+ a[n - 1] + b[n - 1] = cnt(n - 1) + b[n - 1] = cnt(n - 1) +? cnt(n - 2)。

此乃斐波那契數列。考慮 cnt(1) = 2 = fib(3)，則 cnt(n) = fib(n + 2)。

fib(n)通項公式：

n趨于無窮大時，cnt(n) =?? $\frac{1}{\sqrt{5}}(\frac{1 + \sqrt{5}}{2}) ^{n + 2}$

共有m行，每行枚舉兩遍k，忽略常數項，O( $m(\frac{1 + \sqrt{5}}{2}) ^{n}$ )。

總時間復雜度??O(?+? $m(\frac{1 + \sqrt{5}}{2}) ^{n}$ )。

相鄰兩行遞推

AcWing 327：

司令部的將軍們打算在?N×M 的網格地圖上部署他們的炮兵部隊。

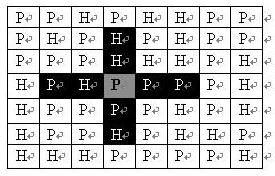
一個?N×M 的地圖由?N 行?M?列組成，地圖的每一格可能是山地（用?H?表示），也可能是平原（用?P?表示），如下圖。

在每一格平原地形上最多可以布置一支炮兵部隊（山地上不能夠部署炮兵部隊）；一支炮兵部隊在地圖上的攻擊范圍如圖中黑色區域所示：

如果在地圖中的灰色所標識的平原上部署一支炮兵部隊，則圖中的黑色的網格表示它能夠攻擊到的區域：沿橫向左右各兩格，沿縱向上下各兩格。

圖上其它白色網格均攻擊不到。

從圖上可見炮兵的攻擊范圍不受地形的影響。

現在，將軍們規劃如何部署炮兵部隊，在防止誤傷的前提下（保證任何兩支炮兵部隊之間不能互相攻擊，即任何一支炮兵部隊都不在其他支炮兵部隊的攻擊范圍內），在整個地圖區域內最多能夠擺放多少我軍的炮兵部隊。

輸入格式

第一行包含兩個由空格分割開的正整數，分別表示?N?和?M；

接下來的?NN?行，每一行含有連續的?M?個字符(P?或者?H)，中間沒有空格。按順序表示地圖中每一行的數據。

輸出格式

僅一行，包含一個整數?K，表示最多能擺放的炮兵部隊的數量。

數據范圍

N≤100,M≤10

輸入樣例：
5 4
PHPP
PPHH
PPPP
PHPP
PHHP
輸出樣例：
6

這次變成了兩行遞推。?

思路

只需要對上次的代碼稍作修改。

dp[i & 1][k1][k2]?表示 [0,?i] 行且第 i 行狀態為 k1，第 i - 1 行狀態為 k2 的最值。

三個約束：

k 要服從地圖的約束，也就是第 i 行的合法 k 僅能是 g[i] 的子集。
k 內不含有相鄰1或相間一個0，也就是行內需要合法。
第 i 行 k 也不能與 i - 1 行和 i - 2k 不含有相鄰1，也就是兩行間需要合法。

算法過程

行內合法的條件是：?(k & (k >> 1) == 0 && ?(k & (k >> 2) == 0。

符合地圖約束的k的條件：(k | g[i]) == g[i]。
行間合法的條件是：(k1 & k2) == 0 && (k1 & k3) == 0?&& (k2 & k3) == 0 。

Code

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 100, M = 10, MOD = 1e8;
int m, n, mx;
int g[N], dp[2][1 << M][1 << M], cnt[1 << M];
vector<int> st;
bool check(int k){return !(k & (k >> 1)) && !(k & (k >> 2));
}
bool check(int a, int b){return !(a & b);
}
int solve(){for (int k = 0; k <= mx; k++)if (check(k)) {st.push_back(k);cnt[k] = bitset<M>(k).count();}for (int k1 : st) if ((k1 | g[0])== g[0]) {dp[0][k1][0] = cnt[k1];for (int k2 : st) if ((k2 | g[1])== g[1] && check(k1, k2))dp[1][k2][k1] = cnt[k1] + cnt[k2];}for (int i = 2; i <= n + 1; i++)for (int k1 : st) if ((k1 | g[i]) == g[i])for (int k2 : st) if ((k2 | g[i - 1]) == g[i - 1] && check(k1, k2)) {dp[i & 1][k1][k2] = 0;for (int k3 : st) if ((k3 | g[i - 2]) == g[i - 2] && check(k1, k3) && check(k2, k3))dp[i & 1][k1][k2] = max(dp[i & 1][k1][k2], dp[(i - 1) & 1][k2][k3] + cnt[k1]);}return dp[(n + 1) & 1][0][0];
}
int main(){cin >> n >> m;  mx = (1 << m) - 1;for (int i = 0; i < n; i++)for (int j = 0; j < m; j++) {char x; cin >> x;g[i] |= ((x == 'P') << j);}cout << solve();return 0;
}

復雜度

時間復雜度:?O(?+? $mT ^{n}$ )

空間復雜度:?O( $2^{n}$ )?

T：常數，1 < T <? $\frac{1 + \sqrt{5}}{2}$

n：列數

m：行數

特殊優化：編譯期計算

以第一題為例，我們知道 k 可以預處理得到，那能否更進步一些呢？?

C++提供大量的靜態計算支持，我們可以利用C++特性做一些工作。

我們直接在編譯期計算 k 的合法狀態，constexpr 函數會嘗試進行編譯期計算，我們傳入編譯期常量 N，就會在編譯期直接生成出合法狀態的數組。

雖然表面上我們是在編譯期調用計算函數，但其實它已經算好了，已經儲存在可執行程序中，這就省去了一個O()。

運行期由于每次數據范圍不同，可以二分得到 k 的上界，然后正常計算即可。

constexpr int N = 13, MOD = 1e8;
int m, n, mx;
int g[N], dp[2][1 << N];
constexpr pair<array<int, 1 << N>, int> get_st(int MX){array<int, 1 << N> st{};int st_size = 0;for (int k = 0; k < MX; k++)if (!(k & (k >> 1)))st[st_size++] = k;return {st, st_size};
}
constexpr auto s = get_st(1 << N);
constexpr auto st = s.first;
constexpr auto st_size = s.second;
int solve(){int upper = upper_bound(st.begin(), st.begin() + st_size, mx) - st.begin();for (int k = 0; k < upper; k++)if ((st[k] | g[0]) == g[0])dp[0][st[k]] = 1;for (int i = 1; i <= m; i++)for (int k = 0; k < upper; k++) {dp[i & 1][st[k]] = 0;for (int pre_k = 0; pre_k < upper; pre_k++)if (!(st[k] & st[pre_k]) && (st[k] | g[i]) == g[i])dp[i & 1][st[k]] = (dp[i & 1][st[k]] + dp[(i - 1) & 1][st[pre_k]]) % MOD;}return dp[m & 1][0];
}