01背包問題基礎

1. 暴力解法

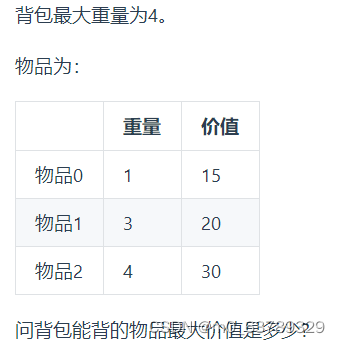
每個物品有兩種狀態，放與不放，可通過回溯暴力求解，復雜度為N(2的n次方)

2. 二維dp數組01背包

1.確定dp數組以及下標的含義

對于背包問題，有一種寫法， 是使用二維數組，即dp[i][j] 表示從==，下標為==[0-i]==的物品里任意取，放進容量為j的背包，價值總和最大是多少。
![在這里插入圖片描述](https://img-blog.csdnimg.cn/f1dd9f281aca4f8a8c06bee3aece4b64.png

2.遞推公式

• 放物品 i : 不放物品 i 時的最大價值加上放物品 i 的價值 ：dp[i - 1][j - weight[ i ]] + value[ i ]；
• 不放物品i ：dp[i - 1][j]推出，當前背包容量為 j ，
• 遞推公式：dp[i ][j] = max(dp[i - 1][j]，dp[i - 1][j - weight[ i ]] + value[ i ])

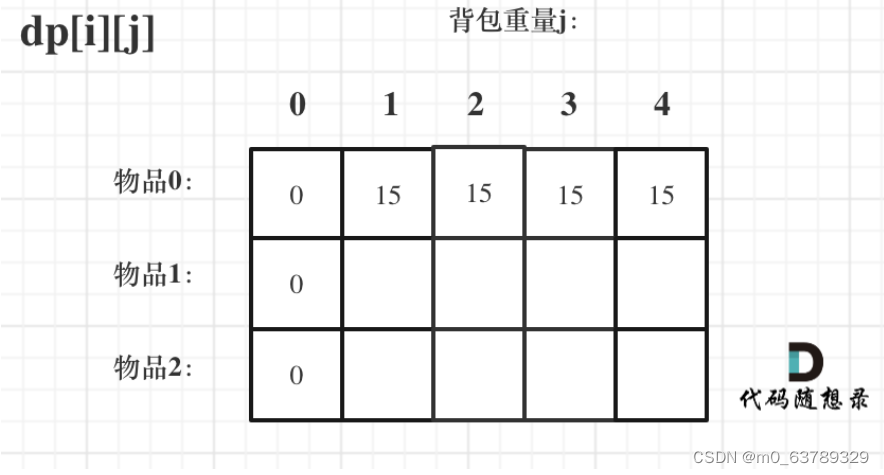
3.dp數組如何初始化

初始化第一列，背包容量為0，則價值都為0
初始化第一行，物品為0，當背包為0 時放不了所有價值為0；當背包為1時剛好放下物品，所有價值為15；后序同理為15
非零下標：初始化值不影響

vector<vector<int>>dp(weight.size(), vector<int>(bagweight + 1, 0));
for (int j = 0 ; j < weight[0]; j++) {  // 當然這一步，如果把dp數組預先初始化為0了，這一步就可以省略，但很多同學應該沒有想清楚這一點。dp[0][j] = 0;
}
// 正序遍歷
for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];
}

4.遍歷順序

二維dp可以先遍歷物品也可先遍歷背包
為什么？
因為：遞歸公式中可以看出dp[i][j]是靠dp[i-1][j]和dp[i - 1][j - weight[i]]推導出來的。dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向（包括正上方向），那么先遍歷物品，再遍歷背包的過程如圖所示：
雖然兩個for循環遍歷的次序不同，但是dp[i][j]所需要的數據就是左上角，根本不影響dp[i][j]公式的推導！

// weight數組的大小 就是物品個數
for(int i = 1; i < weight.size(); i++) { // 遍歷物品for(int j = 0; j <= bagweight; j++) { // 遍歷背包容量if (j < weight[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}
}

5.測試代碼

void test_2_wei_bag_problem1() {vector<int> weight = {1, 3, 4};vector<int> value = {15, 20, 30};int bagweight = 4;// 二維數組vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));// 初始化for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];}// weight數組的大小 就是物品個數for(int i = 1; i < weight.size(); i++) { // 遍歷物品for(int j = 0; j <= bagweight; j++) { // 遍歷背包容量if (j < weight[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}}cout << dp[weight.size() - 1][bagweight] << endl;
}int main() {test_2_wei_bag_problem1();
}

01背包理論基礎（滾動數組）：將二維dp轉換為一維dp

1. dp數組以及下標名義

dp[j]：容量為j的背包所能裝的最大價值。

2. 遞歸公式

• 不放物品i ：dp[j]可以由dp[j - weight[i]]推出，當前背包容量為 j ，

• 放物品 i : 不放物品 i 時的最大價值加上放物品 i 的價值 ：dp[j - weight[ i ]] + value[ i ]；

• 遞推公式：max(dp[j], dp[j - weight[ i ]] + value[ i ])入代碼片

3. dp數組如何初始化

dp[0] = 0
非零下標：dp數組在推導過程中一定是取價值最大的數，如果題目給的價值都是正整數那么非零下標都初始化為0就可以了，這樣才能讓dp數組在遞推公式的過程中取得最大的價值，而不是被初始值覆蓋掉

4. 遍歷順序:從后往前遍歷

for(int i = 0; i < weight.size(); i++) {//遍歷物品for(int j = bageweight; j >= weight[i]; j--) {//遍歷背包容量dp[j] = max(dp[j], dp[j - weight[ i ]] + value[ i ]);}
}

倒序原因，
舉例如下表，weight[0] = 1, 價值 value[0] = 15,如果正序遍歷

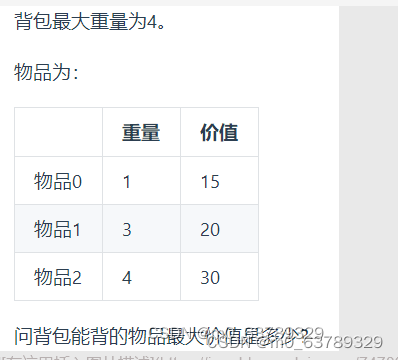
正序
dp[1] = dp[1 - weight[0]] + value[0] = 15
dp[2] = dp[2 - weight[0]] + value[1] = 30  此時物品0 被放了兩次倒序，先計算dp[2]
dp[2] = dp[2 - weight[0]] + value[1] = 15  因為初始化了dp[1]為0
dp[1] = dp[1 - weight[0]] + value[0] = 15

為什么倒序
倒序遍歷的原因是，本質上還是一個對二維數組的遍歷，并且右下角的值依賴上一層左上角的值，因此需要保證左邊的值仍然是上一層的，從右向左覆蓋。
為什么二維數組不用倒序
因為對于二維dp，dp[i][j]都是通過上一層即dp[i - 1][j]計算而來，本層的dp[i][j]并不會被覆蓋！
為什么不可以先遍歷背包再遍歷物品
因為一維dp的寫法，背包容量一定是要倒序遍歷，如果遍歷背包容量放在上一層，那么每個dp[j]就只會放入一個物品，即：背包里只放入了一個物品。

5.一維dp01背包完整C++測試代碼

void test_1_wei_bag_problem() {vector<int> weight = {1, 3, 4};vector<int> value = {15, 20, 30};int bagWeight = 4;// 初始化vector<int> dp(bagWeight + 1, 0);for(int i = 0; i < weight.size(); i++) { // 遍歷物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍歷背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}}cout << dp[bagWeight] << endl;
}int main() {test_1_wei_bag_problem();
}

416. 分割等和子集

首先，本題要求集合里能否出現總和為 sum / 2 的子集

1. dp數組以及下標名義

dp[j]：容量為j的背包所能裝的最大價值。

2. 遞歸公式

-本題相當于背包里放入數值，那么物品i的重量是nums[i]，其價值也是nums[i]。

• 遞推公式：max(dp[j], dp[j - nums[i]] + nums[i])入代碼片

3. dp數組如何初始化

dp[0] = 0
非零下標：dp數組在推導過程中一定是取價值最大的數，如果題目給的價值都是正整數那么非零下標都初始化為0就可以了，這樣才能讓dp數組在遞推公式的過程中取得最大的價值，而不是被初始值覆蓋掉

/ 總和不會大于20000，背包最大只需要其中一半，所以10001大小就可以了
vector<int> dp(10001, 0);

4. 遍歷順序:從后往前遍歷

5. 代碼

class Solution {
public:bool canPartition(vector<int>& nums) {vector<int>dp(10001 , 0);int sum = 0;for(int i = 0; i < nums.size(); i++) {sum +=nums[i];}if(sum % 2 == 1)return false;for (int i = 0; i < nums.size(); i++) {for(int j = sum/2; j >= nums[i]; j--) {dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);}}if(dp[sum/2] == sum / 2)return true;return false;}
};